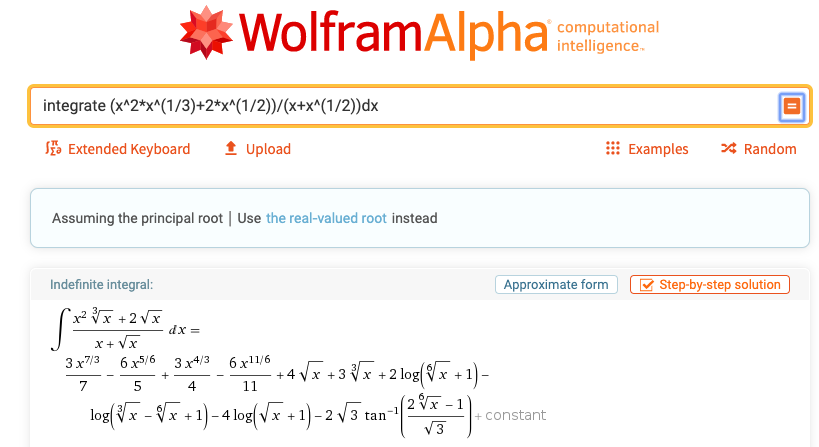
f(x)=(x^(7/3)+2*x^(1/2))/(x+x^(1/2))=2*x^(1/2)/(x+x^(1/2))+g(x)
u=x^(1/6); u'=1/(6*x^(5/6))=> du=dx/(6*x^(5/6))
g(x)=x^(7/3)/(x+x^(1/2))=u^14/(u^6+u^3); dx=(6*u^5)*du
g(x) dx=(((u^14/(u^6+u^3))*(6*u^5))*du+
+(2*(u+1)/(u^2-u+1)-2*(u+1)/(u^2-u+1))*du
h(u)=-2*(u+1)/(u^2-u+1))=(1-2*u)/(u^2-u+1)-3/(u^2-u+1)=(1-2*u)/(u^2-u+1)+s(u)
v=(u-1/2)*2/sqrt(3); u=sqrt(3)*v/2+1/2; du=sqrt(3)*dv/2
s(u)=-3/(u^2-u+1)=-3/((sqrt(3)*v/2+1/2)^2-sqrt(3)*v/2-1/2+1)=-4/(v^2+1)
s(u)du=(-2*sqrt(3)/(v^2+1))*dv